저번 글에서 동일 비중으로 우리가 들어본 듯한 회사들을 구성하여 기술주, 은행주, 배당주 10개만 적당히 굴려도 괜찮은 퍼포먼스(연평균 단순 기대수익률 33%, 리스크 21%, Sharpe Ratio는 1.56)가 나오는 결과를 얻었습니다. 이번 시간에는 조금 더 많은 시뮬레이션을 통해 비중을 최적화시켜 수익률을 개선시키고 리스크를 줄이는 방법에 대해 이야기해보겠습니다.
저번 글의 코드가 이어지니 참고하시면 좋겠습니다.
daily_ret = df.pct_change() # 2013년 1월 1일 ~ 2021년 8월 27일까지 10종목 수정 종가데이터의 일별주가상승률
annual_ret = daily_ret.mean() * 252 # 연평균 주가상승률
daily_cov = daily_ret.cov() # 일별주가상승률의 공분산행렬
annual_cov = daily_cov * 252 # 공분산행렬에서 영업일 수를 곱함
# 포트폴리오의 일별주가상승률, 리스크, 비중, Sharpe Ratio를 빈 리스트로 세팅
port_ret = []
port_risk = []
port_weights = []
sharpe_ratio = []
저번 글의 10개의 종목들을 불러와 위와 같이 세팅을 합니다. 이제 포트폴리오를 가상으로 30만개를 랜덤으로 만들 예정입니다.
for _ in tqdm(range(300000)): # ①
weights = np.random.random(len(tickers))
weights /= np.sum(weights) # ②
returns = np.dot(weights, annual_ret) # ③
risk = np.sqrt(np.dot(weights.T, np.dot(annual_cov, weights))) # ④
# ⑤
port_ret.append(returns)
port_risk.append(risk)
port_weights.append(weights)
sharpe_ratio.append(returns/risk)
①은 내가 얼마나 포트폴리오를 임의로 만들 것인가에 대한 숫자입니다. (티커 수(종목 수)가 많을 수록 시뮬레이션을 돌릴 때 컴퓨터가 고통을 받을 것입니다.)
이전 글에서는 0.1(10%)씩 동일비중으로 가중치를 부여했었지만 ②는 numpy의 random을 이용해서 10개의 티커들의 임의의 가중치를 랜덤으로 부여한다는 뜻입니다.
③은 가중치와 연 수익률 행렬과 내적을 실시하고 ④는 포트폴리오의 변동성의 기댓값을 산출합니다.

30만 개의 포트폴리오에 대한 수익률, 변동성의 기댓값, 가중치, Sharpe Ratio들이 list에 저장이 됩니다. 이제 pandas를 이용해서 정보들을 데이터프레임에 아래처럼 적재를 합니다.
portfolio = {'Returns': port_ret, 'Risk': port_risk, 'Sharpe': sharpe_ratio}
for i, s in enumerate(tqdm(tickers)):
portfolio[s] = [weight[i] for weight in port_weights]
df = pd.DataFrame(portfolio)
df = df[['Returns', 'Risk', 'Sharpe'] + [s for s in tickers]]
이제 df에는 30만 개의 포트폴리오 정보들이 있습니다.

파란색으로 영역을 표시한 곳은 각 포트폴리오의 연평균 수익률(Returns), 변동성(Risk), Sharpe Ratio(Sharpe)들의 정보가 있고, 빨간색으로 영역을 표시한 곳은 각 포트폴리오의 종목들의 비중들에 대한 정보들이 있습니다. 여기서 본인 성향에 따라서 정할 수 있습니다.
ⓐ 나는 리스크가 제일 작은 포트폴리오로 구성하고 싶어요.
ⓑ 조금 잃어도 괜찮으니까 나는 리스크 대비 수익률을 최대한 높여보고 싶어요.
min_risk = df.loc[df['Risk'] == df['Risk'].min()] # ⓐ
max_sharpe = df.loc[df['Sharpe'] == df['Sharpe'].max()] # ⓑ
각각의 질문에 맞는 포트폴리오는 위와 같이 돌리면 찾을 수 있습니다.

ⓐ는 단순 연평균 수익률이 23.6%, ⓑ는 단순 연평균 수익률이 45.7% 임을 알 수 있습니다. ⓐ 포트폴리오는 상대적으로 배당성향이 강한 SBUX, MAIN이 비중이 큼을 대략적으로 알 수 있고, ⓑ는 퍼포먼스가 좋은 성장주 위주(TSLA, AMZN)로 구성되어 있음을 알 수 있습니다. 아래 그림을 한번 확인해 보겠습니다.
df.plot.scatter(x='Risk', y='Returns', c='Sharpe', cmap='viridis',
edgecolors='k', figsize=(11,7), grid=True)
plt.scatter(x=max_sharpe['Risk'], y=max_sharpe['Returns'], c='r',
marker='*', s=300)
plt.scatter(x=min_risk['Risk'], y=min_risk['Returns'], c='r',
marker='X', s=200)
plt.title('Portfolio Optimization')
plt.xlabel('Risk')
plt.ylabel('Expected Returns')
plt.show()
x축은 왼쪽으로 갈수록 변동성이 작아집니다. y축은 기대수익률입니다. 색깔은 Sharpe Ratio를 뜻합니다. 30만 개의 포트폴리오를 시뮬레이션을 했을 때 X 표시가 최소 Risk, ☆표시가 최대 Sharpe Ratio인 포트폴리오입니다. 저번 글에서 동일비중으로 했을 때 퍼포먼스는 연평균 단순 기대수익률 33%, 리스크 21%, Sharpe Ratio는 1.56이었습니다. 이번 Sharpe Ratio가 1.70이 나오므로 조금 더 개선된 포트폴리오라고 할 수 있습니다. Sharpe Ratio가 최대인 포트폴리오는 티커와 가중치를 아래와 같이 정리할 수 있습니다.
stock_weight_dict = dict(zip(list(max_sharpe[tickers].columns),
max_sharpe[tickers].values.flatten().tolist()))
stock_weight_dict
from collections import OrderedDict
weights = OrderedDict(stock_weight_dict)
pd.Series(weights).plot.barh();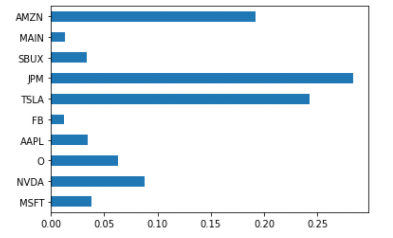
랜덤으로 뽑다 보니 JPM이 비중이 제일 높은 게 마음에는 들진 않지만 13년 1월 2일부터 21년 8월 27일까지 기준으로 위와 같은 구성으로 리밸런싱 없이 포트폴리오를 구성했을 때 리스크 대비 수익률이 좋았다는 뜻입니다.
만약에 마지막 종가 기준(21.8.27)으로 10,000달러를 들고 있을 때 거치식으로 포트폴리오를 위와 같이 구성한다면 몇 줄을 사는 게 좋은지 확인해보겠습니다.
from pypfopt import DiscreteAllocation
latest_prices = prices.iloc[-1] # 마지막 종가 기준
da = DiscreteAllocation(weights, latest_prices, total_portfolio_value=10000)
alloc, leftover = da.lp_portfolio()
print(f"Discrete allocation performed with ${leftover:.2f} leftover")
alloc
애플을 2주 매수, 아마존을 3주 매수하는 식으로 위의 dictionary 결과만큼 구성하면 134달러가 예수금으로 남는다는 뜻입니다.
<정리>
본인 입맛에 맞게 사고 싶은 종목들을 구성한다면 이전 글과 이번 글을 통해 참고 정도는 받을 수 있을 것입니다. 동일 비중으로 구성한 포트폴리오, 비중을 최적화한 포트폴리오 컨셉은 상당히 다양합니다. 매수, 매도 의견은 아니지만 제가 수시로 매매를 하는 FNGU, BULZ와 같은 ETN은 동일 비중으로 기술주들을 구성하였고 다른 ETF들은 비중을 유연하게 가져가면서 또한 주기적으로 리밸런싱을 합니다.
제가 블로그에 쓴 글의 단점은 리밸런싱이 없습니다. 또한 배당금을 받으면 재투자하는 방식의 전략도 포함되어 있지 않습니다. 이렇게 최적화하는 방식은 과거 10년 정도는 통했지 이 방식이 미래의 수익을 보장하지 않습니다. 실제로 제가 위와 같은 방식으로 투자할 것이냐고 물어보신다면 참고만 할 뿐, 리스크 20% 이상을 견디기 힘들 것 같아 저는 아마 하지 않을 것 같습니다.(저는 심법을 더 단련해야 합니다.) 주식 안에서 최대한 분산투자를 한 것이지 채권이나 금, 은같은 다른 자산군에 투자를 한 것도 아닙니다.
Risk에는 체계적 위험과 비체계적 위험이라는 것이 존재합니다. 체계적 위험이라고 하면 내가 통제할 수 없는, 제어할 수 없는 외부 요인들을 뜻합니다. 자연재해나 전쟁도 있을 것이고 거시 경제 요인으로 인플레이션이나 시장에 불안 요소 등 이런 위험들은 자산 배분으로 최대한 자산을 방어해야 합니다. 비체계적 위험은 특정 회사 또는 산업, 비즈니스, 재무 등의 위험요소들을 뜻합니다.

앞서 소개한 이러한 포트폴리오들은 개별종목들의 분산은 적어도 비체계적 위험을 줄일 수 있습니다. 이런 글을 읽는 분들에게 조금이나마 자산을 지키는데 도움이 되었으면 좋겠습니다. 다음 글은 python 코드 없이 포트폴리오를 백테스팅할 수 있는 high-level tool을 소개할 예정입니다.
긴 글 읽어주셔서 감사합니다.
<Reference>
https://ko.gadget-info.com/difference-between-systematic
체계적 위험과 비 체계적 위험의 차이
체계적 위험과 체계적 위험의 차이를 알면이 두 용어를 더 잘 이해할 수 있습니다. 체계적인 위험은 거시 경제 요인으로 인해 발생합니다. 반면에 체계적이지 않은 위험은 미시 경제 요인으로
ko.gadget-info.com
https://randerson112358.medium.com/python-for-finance-portfolio-optimization-66882498847
Python For Finance Portfolio Optimization
Portfolio optimization is the process of selecting the best portfolio (asset distribution),out of the set of all portfolios being…
randerson112358.medium.com
https://hotorch.tistory.com/58?category=1033008
자산 배분 포트폴리오 - 4. 동일 비중 포트폴리오
Python이라는 도구를 활용해서 직전 글(아래 Reference) 막바지에 소개한 10 종목을 바탕으로 어떻게 포트폴리오를 구성하는지, 이렇게 구성했을 때 어떤 구조를 가지게 되는지 알아보고자 합니다. !p
hotorch.tistory.com
'Investment - Stock & Crypto > Quant Strategy' 카테고리의 다른 글
| 자산 배분 포트폴리오 - 7. 포트폴리오 전략 예시 (0) | 2021.10.16 |
|---|---|
| 자산 배분 포트폴리오 - 6. Portfolio Visualizer (0) | 2021.10.10 |
| 자산 배분 포트폴리오 - 4. 동일 비중 포트폴리오 (0) | 2021.08.29 |
| 자산 배분 포트폴리오 - 3. 포트폴리오 성과 지표 (0) | 2021.08.08 |
| 자산 배분 포트폴리오 - 2. 데이터 수집 (0) | 2021.07.25 |
